Mark Hopkins

 COMPUTER SCIENCE, WILLIAMS COLLEGE

I am an Assistant Professor of Computer Science at Williams College. My research focuses on machine learning, knowledge representation, and uncertain reasoning, particularly as applied to natural language tasks. Github: Mark-Hopkins-at-Williams. In the spring, I will be teaching CSCI 381 (Deep Learning). 

Screen Shot 2018-08-18 at 4.13.00 PM

Recent Research Highlights

(publication list)

Screen Shot 2020-06-09 at 8.02.57 PM

Transformer Neural Networks for Protein Family and Interaction Prediction Tasks. (Journal of Computational Biology 2022): We adapt natural language processing techniques to the automatic identification of protein families. (pdf)

testperanto_screenshot

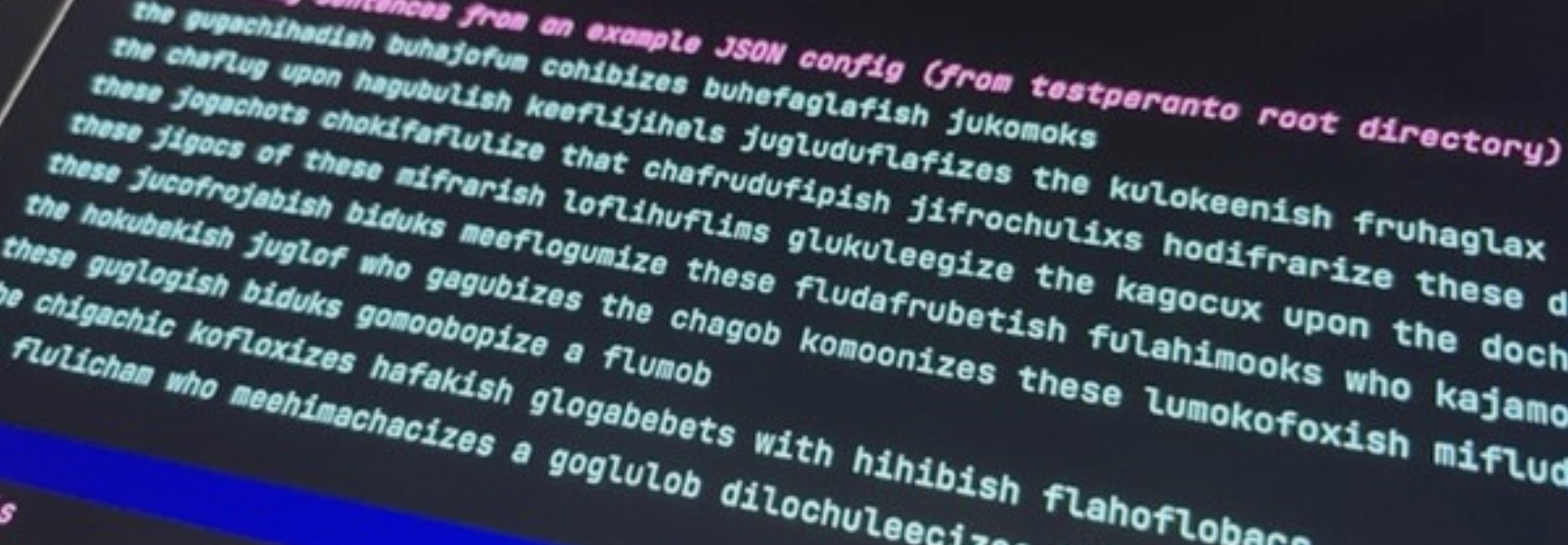
Towards More Natural Artificial Languages (CoNLL 2022):  Artificial languages have the potential to enable the targeted study of how typological properties of language impact model performance. In this work, we enhance the realism of artificial languages by developing a generation method that supports selectional preference. (pdf) (code)

Screen Shot 2023-07-09 at 5.56.18 PM

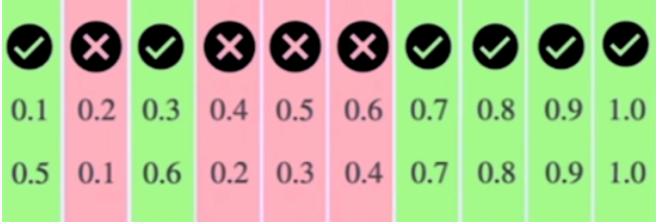
On the Evaluation of Neural Selective Prediction Methods for Natural Language Processing (ACL 2023): We consider what it takes to determine whether an NLP system is good at keeping silent when it is wrong. (pdf)

Screen Shot 2018-06-22 at 12.23.34 PM

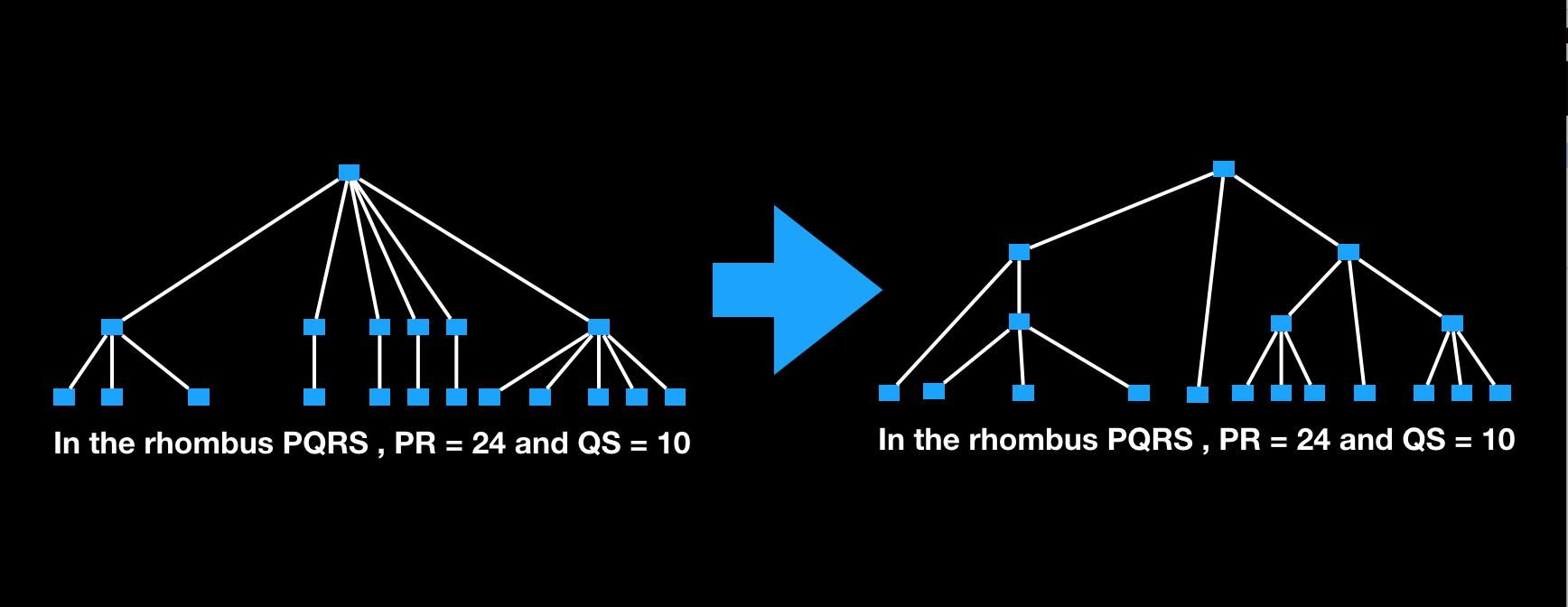
Extending a Parser to Distant Domains Using a Few Dozen Partially Annotated Examples (ACL 2018): We revisit domain adaptation for parsers in the neural era. (pdf)

Screen Shot 2020-06-09 at 8.52.02 PM

Reed at SemEval-2020 Task 9: Fine-Tuning and Bag-of-Words Approaches to Code-Mixed Sentiment Analysis (SemEval 2020): We explore sentiment analysis on code-mixed Hindi-English tweets as participants of Task 9 of the SemEval-2020 competition, in which Reed College placed fourth (out of 62 teams). (pdf)

Screen Shot 2018 06 22 at 11.04.33 AM

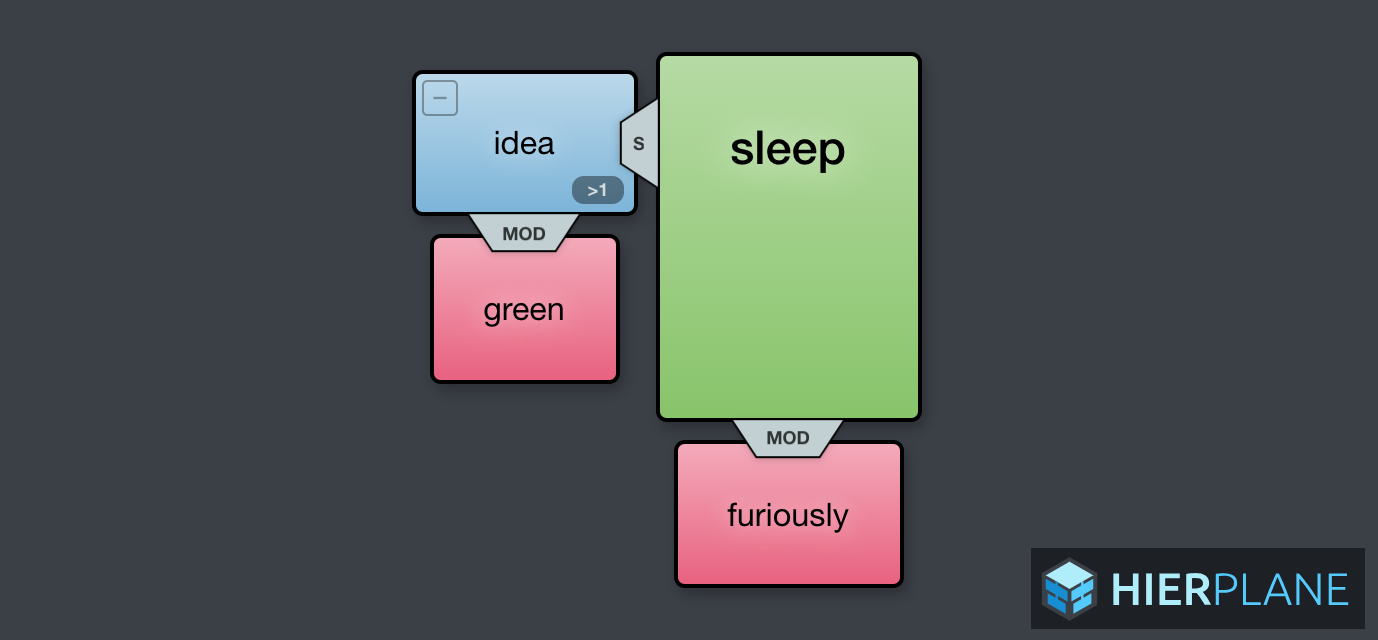
Odd Man Out: Exploring the Associative Power of Lexical Resources (EMNLP 2018): A simple task, determining the “odd-man-out” from a set of choices, can be an effective means of comparing and contrasting the power of taxonomies and vector embeddings. (pdf)

Teaching

CSCI 373: Artificial Intelligence (Spring 2023, course page): Artificial Intelligence (AI) has become part of everyday life, but what is it, and how does it work? This course introduces theories and computational techniques that serve as a foundation for the study of artificial intelligence. 

CSCI 381: Deep Learning (Spring 2024, course page): This course is an introduction to deep neural architectures and their training. Beginning with the fundamentals of regression, optimization, and regularization, the course will then survey a variety of architectures and their associated applications.

 

Previous courses:

  • CSCI 134 (Introduction to Computer Science): Spring 2023, Fall 2023
  • CSCI 121 (Fundamentals of Computer Science, at Reed College): Fall 2018, Spring 2019, Fall 2019, Spring 2020, Spring 2021
  • CSCI 377 (Artificial Intelligence, at Reed College): Fall 2018, Fall 2020
  • CSCI 378 (Deep Learning, at Reed College): Spring 2019, Spring 2020